Т.Ю. Овсянникова
Экономика строительного комплекса: Экономическое обоснование и реализация инвестиционных проектов
Учебное пособие – Томск: Изд-во Томск. гос. архит.-строит. ун-та, 2003. – 239 с. 5. Эффективность инвестиций
5.5. Учет инфляции в расчетах эффективности
Инфляция – это рост цен на товары и услуги. Инфляция
является важнейшим индикатором макроэкономического развития и одним из основных
факторов, влияющих на эффективность инвестиционного процесса.
Выше, говоря об изменении временнóй стоимости
денежных потоков, мы учитывали только влияние на стоимость денег их собственной
способности «прирастать в деле», т.е. изменять свою стоимость в процессе
оборота. Рассмотрим теперь, каким образом на временнóй стоимости
денежных потоков сказывается инфляция.
Золотое правило инвестирования гласит: «не имеет
смысла вкладывать деньги в проект, доходность которого ниже уровня инфляции».
Международная практика проектного анализа допускает
расчет эффективности инвестиций без учета влияния инфляции, если инфляция
незначительна и постоянна. Однако при этом не учитываются потери инвестора в
связи с инфляцией.
Влияние инфляции проявляется, прежде всего, в
увеличении денежных потоков за счет изменения всех ценовых показателей проекта,
изменения (увеличения) общей потребности в инвестициях, необходимых для
реализации проекта (особенно для объектов с длительным инвестиционным циклом),
что, в конечном счете, сказывается на показателях эффективности проекта и
принятии решения о целесообразности его осуществления.
При учете влияния инфляции на эффективность проекта
используются следующие показатели, характеризующие инфляцию:
-
базисный (общий) индекс роста цен  на продукцию, услуги и используемые
ресурсы: на продукцию, услуги и используемые
ресурсы:
 , (5.28) , (5.28)
-
цепной индекс роста цен  на продукцию, услуги и используемые
ресурсы: на продукцию, услуги и используемые
ресурсы:
 , (5.29) , (5.29)
-
уровень инфляции 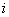 : :
 или или  , (5.30) , (5.30)
где
 – уровень цен в период времени t , руб.; – уровень цен в период времени t , руб.;
 –
уровень цен в начальный момент времени, руб.; –
уровень цен в начальный момент времени, руб.;
 –
уровень цен в период времени (t-1), руб. –
уровень цен в период времени (t-1), руб.
Учет инфляции в экономической оценке инвестиционных
проектов заключается в следующем:
1.
Пересчет всех ценовых показателей
(денежных потоков) на расчетном шаге t в прогнозные цены с использованием базисных или цепных индексов:
 (5.31) (5.31)
где  –
соответственно, показатели инвестиций, выручки и себестоимости в прогнозных ценах
на шаге t, руб.; –
соответственно, показатели инвестиций, выручки и себестоимости в прогнозных ценах
на шаге t, руб.;
 – себестоимость – себестоимость  го ресурса, используемого в
производстве продукции на шаге t, руб.; го ресурса, используемого в
производстве продукции на шаге t, руб.;
 – прогнозные базисные индексы роста цен для
соответствующего вида денежных потоков. – прогнозные базисные индексы роста цен для
соответствующего вида денежных потоков.
2.
Корректировка нормы дисконта на
уровень инфляции. При уровне инфляции до 10% эту корректировку можно произвести
путем пересчета реальной нормы дисконта (доходности), отражающей минимальные
требования инвестора к доходности инвестиций, в номинальную норму (установленную
в депозитном или кредитном договоре и включающую инфляционные потери):
 , (5.32) , (5.32)
где 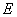 – номинальная
норма дисконта, десятичное измерение; – номинальная
норма дисконта, десятичное измерение;
 – реальная
норма дисконта, десятичное измерение; – реальная
норма дисконта, десятичное измерение;
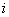 – уровень
инфляции (в этих расчетах уровень инфляции рассчитывается в десятичном измерении,
как и норма дисконта). – уровень
инфляции (в этих расчетах уровень инфляции рассчитывается в десятичном измерении,
как и норма дисконта).
Если уровень инфляции > 10% в год, то есть  ,
то определение ставки дисконтирования должно осуществляться по формуле И.
Фишера: ,
то определение ставки дисконтирования должно осуществляться по формуле И.
Фишера:
 , (5.33) , (5.33)
полученной
из соотношения:
 . (5.34) . (5.34)
При малом уровне инфляции результаты, полученные по
формулам (5.32) и (5.33), дают практически одинаковый результат, что позволяет
использовать формулу (5.32) как более простую. Однако при высоком уровне
инфляции погрешность при расчете по этим формулам в виде слагаемого   оказывается
существенной, что искажает результат инвестиционного анализа. оказывается
существенной, что искажает результат инвестиционного анализа.
Рассмотрим это на примере:
Инвестор предполагает получить реальную доходность на
вложенный капитал 5% в год при уровне инфляции 6%. Какова должна быть
номинальная норма доходности при оценке эффективности инвестиций?
Решение.
Дано: . .
Номинальная норма дисконта по формуле (5.32):
 . .
Номинальная норма дисконта по формуле (5.33):
 . .
Как видим, разница в полученных результатах небольшая
и величиной 0,003 мы можем пренебречь.
Рассмотрим теперь аналогичную задачу, но при других
исходных данных:
Инвестор предполагает получить реальную доходность на
вложенный капитал 5% в год при уровне инфляции 16%. Какова должна быть
номинальная норма доходности при оценке эффективности инвестиций?
Решение.
Дано: . .
Номинальная норма дисконта по формуле (5.32):
 . .
Номинальная норма дисконта по формуле (5.33):
 . .
Мы видим, что в данном примере отклонение в полученных
результатах уже существеннее и эта разница тем больше, чем выше требуемая
инвестором реальная норма доходности и уровень инфляции. Это подтверждает
необходимость расчета нормы дисконта при высоком уровне инфляции по формуле
И.Фишера.
С учетом оценки инфляционного влияния на показатели
эффективности инвестиционного проекта основная расчетная формула чистого
дисконтированного дохода примет вид:
 , (5.35) , (5.35)
где  – соответственно,
индексы роста цен на денежных потоках, отражающих, соответственно, результаты и
затраты инвестиционного процесса. – соответственно,
индексы роста цен на денежных потоках, отражающих, соответственно, результаты и
затраты инвестиционного процесса.
Поскольку инвестиционным проектом может быть
предусмотрено производство нескольких видов продукции и использование
нескольких видов ресурсов, то формулу (5.35) можно записать в более подробном
виде:
 , (5.36) , (5.36)
где  –
соответственно, результат, получаемый от –
соответственно, результат, получаемый от го
вида продукции, и затраты го
вида продукции, и затраты  го вида ресурсов в
базисных ценах на шаге го вида ресурсов в
базисных ценах на шаге 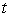 , руб.; , руб.;
 –
соответственно, базисные индексы роста цен на –
соответственно, базисные индексы роста цен на  ую
продукцию и ую
продукцию и  ый вид ресурса на шаге ый вид ресурса на шаге 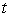 , ,
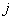 –
вид производимой продукции, –
вид производимой продукции,  ; ;
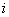 –
вид используемого ресурса, –
вид используемого ресурса,  . .
|

