|
Д.А. Кривошеин, Л.А. Муравей, Н.Н. Роева, О.С. Шорина, Н.Д. Эриашвили, Ю.Г. Юровицкий, В.А. Яковлев
Экология и безопасность жизнедеятельности
Учебное пособие для вузов / Под ред. Л.А. Муравья. – М.: ЮНИТИ-ДАНА, 2000. - 447 с.
Раздел 3. Моделирование в экологии
Глава 9. Динамические модели
9.2. Динамика популяций
В современной экологии часто возникает вопрос: как
определить численность той или иной популяции через определенное время? Ответ
на него не только представляет теоретический, интерес, но и имеет большое
практическое значение. Действительно, не зная этого, нельзя правильно
планировать эксплуатацию различных возобновляемых природных ресурсов –
промысловых рыб, охотничьих угодий и т.п. Может ли в решении этого вопроса
помочь математика? Оказывается, да. Рассмотрим здесь некоторые простейшие
модели, на которых проиллюстрируем подход к данному вопросу.
Пусть некоторая популяция имеет в момент времени t0 биомассу x0.
Предположим, что в каждый момент времени скорость увеличения биомассы
пропорциональна уже имеющейся биомассе, а возникающие явления конкуренции за
источниками питания и самоотравления снижают биомассу пропорционально квадрату
наличной биомассы. Если обозначить биомассу в момент времени t
через х(t), а изменение ее за время 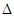 t через t через 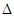 х, то можно записать следующее приближенное
равенство: х, то можно записать следующее приближенное
равенство:
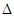 х≈(kх-αх2) х≈(kх-αх2)
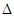 t,
(9.1) t,
(9.1)
где α и k –
положительные постоянные (параметры).
В дифференциальной форме это соотношение имеет вид:
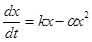 . (9.2) . (9.2)
Оно и представляет собой математическую модель процесса
изменения биомассы популяций. В экологической литературе уравнение (9.2) часто
называют логистическим.
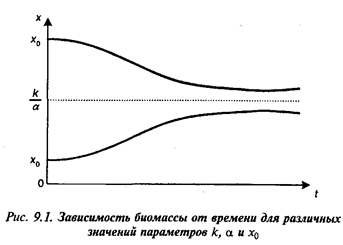
Если теперь поставить вопрос о том, какова же будет биомасса
в момент времени Т, то на него можно ответить экспериментально –
дождаться этого момента и определить биомассу непосредственным измерением
(вообще говоря, такое измерение может быть физически неосуществимым).
Другой путь – воспользоваться математической моделью, решая
задачу Коши для уравнения (9.2) с начальным условием (9.3):
x(t0)=x0. (9.3)
Разделяя в уравнении (9.2) переменные, получим уравнение в
дифференциалах
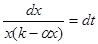 . (9.4) . (9.4)
Для дальнейшего удобно ввести новую переменную
z=αх,
(9.5)
тогда (9.4) можно переписать в виде
 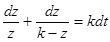 (9.6) (9.6)
Возвращаясь к исходному уравнению (9.2), заметим, что если x0=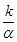 (т. е. z0=k), то задача
Коши имеет решение x(t) (т. е. z0=k), то задача
Коши имеет решение x(t)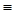 x0 (рис.
9.1). Если x0 < x0 (рис.
9.1). Если x0 <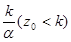 , то уравнение (9.6)
интегрируется следующим образом , то уравнение (9.6)
интегрируется следующим образом
ln z – ln(k-z)=ln z0- ln (k-z0)+k(t-t0),
откуда
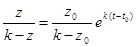 , (9.7) , (9.7)
значит,
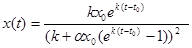 , t >
0 (9.8) , t >
0 (9.8)
Если x0 > 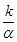 , то аналогично предыдущему случаю снова
получаем формулу (9.8). Дифференцируя (9.8) по t,
имеем , то аналогично предыдущему случаю снова
получаем формулу (9.8). Дифференцируя (9.8) по t,
имеем
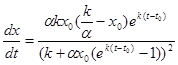 , (9.9) , (9.9)
откуда вытекает, что при x0 < 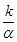 график функции х(t) монотонно возрастает, а при x0> график функции х(t) монотонно возрастает, а при x0>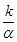 – монотонно убывает, причем оба графика
имеют горизонтальную асимптоту х= – монотонно убывает, причем оба графика
имеют горизонтальную асимптоту х=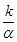 (рис. 9.1). Мы не
приводим здесь элементарную, но громоздкую формулу второй производной d2x/dt2, показывающую, что верхний и нижний
графики имеют по одной точке перегиба. (рис. 9.1). Мы не
приводим здесь элементарную, но громоздкую формулу второй производной d2x/dt2, показывающую, что верхний и нижний
графики имеют по одной точке перегиба.
Мы рассмотрели весьма упрощенную ситуацию, так как
предполагали, что популяция не взаимодействует ни с какими другими популяциями,
учет же этого обстоятельства, конечно, значительно усложняет модель.
Рассмотрим одну из таких моделей. Будем обозначать биомассы
двух популяций через х и у соответственно. Предположим, что обе
популяции потребляют один и тот же корм, количество которого ограничено, и
из-за этого находятся в конкурентной борьбе друг с другом.
Французский математик В. Вольтерра в 1926 г. показал, что
при таком предположении динамика популяций достаточно хорошо описывается
следующей системой дифференциальных уравнений:
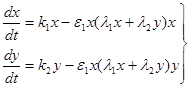 , (9.10) , (9.10)
где 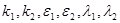 – определенные
положительные числа. – определенные
положительные числа.
Первые члены правых частей системы (9.10) характеризуют
скорость роста популяций при отсутствии ограничивающих факторов. Вторые члены
учитывают те изменения в скоростях, которые вызываются ограниченностью корма.
Задавая различные значения параметров, с помощью системы
(9.10) можно описать взаимодействие двух популяций, одна из которых – хищник, а
другая – жертва [36]. В литературе [47] более подробно описаны математические
аспекты исследования системы (9.10).
Прежде чем исследовать, как будет вести себя система (9.10),
заметим, что в любой момент времени t ее состояние
полностью описывается значениями х и у: каждому состоянию системы
соответствует некоторая точка (х, у) на плоскости хОу, называемой
«фазовой плоскостью». Каждой точке фазовой плоскости можно поставить в
соответствие вектор (стрелку на рис. 9.2) с координатами, которые являются
правыми частями системы, указывающий направление движения в этой точке. Проведя
из начальной точки линии, касательные этим векторам, получим траектории, по
которым будет происходить движение системы, т. е. решения задачи Коши для
системы (9.10) с начальными условиями
x(t0)=x0, y(t0)=y0, (х0,у0)Î х0у. (9.11)
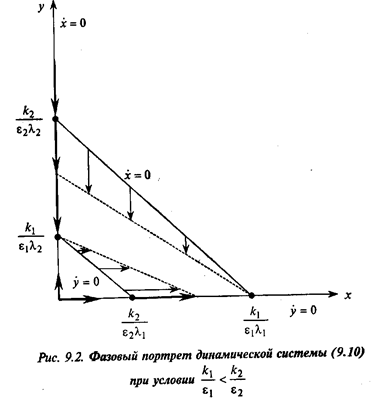
Чтобы составить представление о траекториях движения
системы, построим линии, на которых х=0 (здесь векторы параллельны оси Оу)
и у = 0 (здесь векторы параллельны оси Ох). Для краткости
обозначим производную 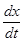 – через х, а – через х, а 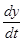 – через у. Имеем – через у. Имеем
х=0, когда 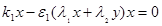 , ,
у=0, когда 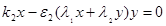 , ,
т. е. х = 0 на двух прямых в фазовой плоскости:
х=0 и 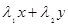 = =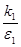 , ,
а у=0 также на двух прямых:
у=0 и 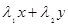 = =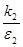 (рис.
9.2, 9.3). (рис.
9.2, 9.3).
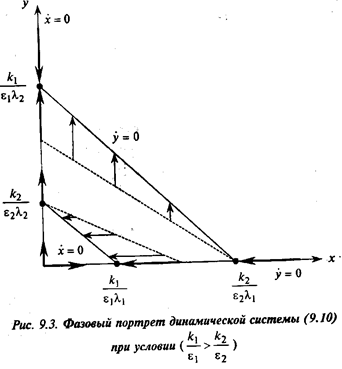
По этим рисункам можно сделать следующие выводы. В обоих
случаях имеем три стационарные точки, в которых одновременно х=0 и у=0,
а именно: (0,0), (0, 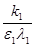 ) и (0, ) и (0, 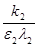 ), которые по известной классификации
являются узлами. При этом, если ), которые по известной классификации
являются узлами. При этом, если 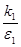 > > 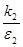 (рис. 9.2), то устойчивым является только
узел ( (рис. 9.2), то устойчивым является только
узел (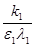 , 0), а если , 0), а если 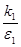 < < 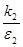 (рис.
9.3), то узел (0, (рис.
9.3), то узел (0, 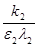 ). Таким образом, если ). Таким образом, если 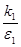 > > 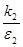 , то
вторая популяция вымирает, y(t) -> 0, t -> , то
вторая популяция вымирает, y(t) -> 0, t -> 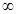 , а первая
стабилизируется, x(t)
-> , а первая
стабилизируется, x(t)
->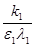 , t -> , t -> . Если же . Если же 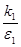 < < 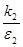 , то
имеем обратную картину: первая популяция вымирает, x(t) -> 0, t-> , то
имеем обратную картину: первая популяция вымирает, x(t) -> 0, t->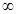 , а вторая стабилизируется, x(t) -> , а вторая стабилизируется, x(t) ->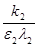 , t-> , t->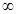 . Наконец, если . Наконец, если 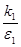 = =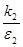 = =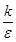 , то кроме неустойчивого узла (0,0) имеем
линию стационарных точек – отрезок прямой , то кроме неустойчивого узла (0,0) имеем
линию стационарных точек – отрезок прямой 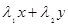 = =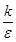 (рис. 9.3). (рис. 9.3).
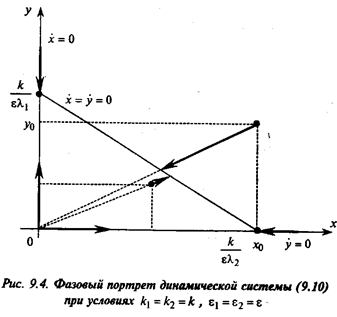
В дальнейших рассмотрениях будем для простоты считать, что k1=k2=k и ε1= ε2= ε.
Тогда, деля второе уравнение системы (9.10) на первое, получим 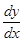 = =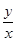 ,
откуда ,
откуда
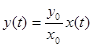 , (9.12) , (9.12)
т. е. траекториями являются отрезки прямых, выходящих из
начала координат (рис. 9.4). Обе популяции не вымирают и численность их
стабилизируется к значениям, которые можно найти как координаты пересечения
прямых 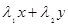 = = 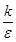 и y = и y = 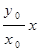 , откуда , откуда
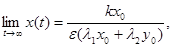 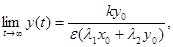 (9.13) (9.13)
|

