Т.Ю. Овсянникова
Экономика строительного комплекса: Экономическое обоснование и реализация инвестиционных проектов
Учебное пособие – Томск: Изд-во Томск. гос. архит.-строит. ун-та, 2003. – 239 с. 5. Эффективность инвестиций
5.3.Временная стоимость денег, текущая и будущая стоимость
Преимущества этого метода заключаются в возможности
учесть изменение временной стоимости денег.
Остановимся еще раз на вопросе о различной
временнóй стоимости денег. Введем для этого два новых понятия: текущая
стоимость (ТС) и будущая стоимость (БС). В зарубежной
экономической литературе эти два термина имеют соответствующие названия: present
value (PV) и future
value (FV).
Допустим, у нас есть тысяча рублей. Стоимость этих
денег сегодня (их текущая стоимость) не равна, как мы уже знаем, их стоимости
завтра (будущей стоимости). И происходит это под действием двух факторов:
-
инфляции, в результате которой
происходит обесценивание денег;
-
оборачиваемости денег, их
способности «прирастать в деле», т.е. приносить доход.
Попробуем определить суть этих экономических
понятий.
ТЕКУЩАЯ СТОИМОСТЬ –
ценность денег в текущий момент времени. Текущая стоимость будущих расходов и
доходов – это их денежный эквивалент в текущем времени.
БУДУЩАЯ СТОИМОСТЬ –
ценность денег в будущем времени. Будущая стоимость доходов и расходов – это их
денежный эквивалент в будущем времени.
Приведение текущей стоимости денег к будущему моменту
времени, т.е. определение их будущей стоимости, называется КОМПАУНДИНГОМ[72].
Приведение будущей стоимости денег к текущему моменту
времени, т.е. определение их текущей стоимости, называется ДИСКОНТИРОВАНИЕМ[73].
Соотношение текущей и будущей стоимости легко увидеть
на схеме (рис. 5.3).

Рис. 5.3. Соотношение
текущей и будущей стоимости денег
Оставим пока в стороне влияние инфляции на
эффективность инвестиций. К этому мы вернемся чуть позже. Рассмотрим изменение
временной стоимости денег лишь вследствие их собственного свойства: способности
оборачиваться и приносить доход.
Решим для иллюстрации изменения временнóй
стоимости денег простую задачу компаундинга:
Инвестор вложил капитал в сумме 20 тыс. руб. в
банковский депозит под 10 % годового дохода. Какой капитал будет иметь
инвестор на депозитном счете через три года при условии рефинансирования
процентов (т.е. проценты, начисленные по вкладу, не будут сниматься с
депозитного счета)?
Посмотрим, как будет изменяться (прирастать) капитал
инвестора по годам.
Через год на депозитном счете инвестора будет капитал
равный
 тыс.
руб. тыс.
руб.
или это можно записать иначе:
 тыс.
руб. тыс.
руб.
Через два года:

 тыс.
руб. тыс.
руб.
Через три года
 тыс.
руб. тыс.
руб.
Итак, мы не только определили, каким капиталом будет
владеть инвестор через три года, но и вывели формулу сложных процентов,
по которой выполняются расчеты в том случае, если проценты, получаемые на
вложенный капитал, реинвестируются, т.е. присоединяются к основному капиталу
(теперь нам понятен смысл слова компаунд – составной, сложный). Формула сложных
процентов является очень важным инструментом финансово-экономического и
инвестиционного анализа. В частности, с её помощью мы установим соотношение
между текущей стоимостью и будущей стоимостью денежных потоков:
 или или  , (5.10) , (5.10)
где  –
норма доходности (норма дисконта), десятичное выражение. –
норма доходности (норма дисконта), десятичное выражение.
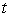 – количество
периодов времени, в течение которого происходит накопление дохода, год (квартал,
месяц). – количество
периодов времени, в течение которого происходит накопление дохода, год (квартал,
месяц).
Экономический смысл этой формулы легко
просматривается: если сегодня мы инвестируем некоторый капитал, имеющий текущую
стоимость ТС, то при годовой доходности инвестиций равной Е, мы будем
иметь через t лет капитал, стоимость которого будет равна БС. Как
в нашем примере, инвестировав под 10 % годовых 20 тыс. руб., мы через три года
будем иметь капитал 26,62 тыс. руб.:

Из формулы (5.9) видно, что
 или или  . (5.11) . (5.11)
Это означает, что если в будущем в некотором году t
мы предполагаем иметь определенный капитал, то его будущая стоимость БС
могла бы быть получена путем инвестирования сегодня капитала стоимостью ТС на
период времени t при годовой доходности, равной Е.
Здесь  – коэффициент
дисконтирования, а – коэффициент
дисконтирования, а  – коэффициент компаундинга
(коэффициент наращения)[74]. – коэффициент компаундинга
(коэффициент наращения)[74].
Соответственно, формула (5.9) является основой задач
компаундинга, а формула (5.10) является основой задач дисконтирования. В
инвестиционном анализе большее применение имеет задача дисконтирования, в
которой инвестор, зная сумму инвестируемого сегодня капитала (текущую
стоимость денег), может оценить стоимость предполагаемых завтра доходов
(будущую стоимость денег), сопоставив их в одной временнóй размерности –
в текущем времени.
Значение коэффициента дисконтирования всегда меньше
единицы, и чем дальше год t от начального момента времени, тем его
значение меньше, а значит, тем меньше текущая стоимость будущих доходов. На
простом примере это можно интерпретировать так: миллион рублей, который мы
будем иметь через год, будет стоить значительно меньше, чем миллион рублей,
который мы имеем сегодня: ведь для того, чтобы получить миллион рублей через
год, нам достаточно инвестировать сегодня 909091 руб. при доходности 10 %:
 руб. руб.
Норма доходности (норма дисконта) Е показывает скорость
изменения стоимости денежных потоков. В задачах компаундинга Е
показывает скорость возрастания стоимости (норма доходности), а в задачах
дисконтирования Е показывает скорость уменьшения стоимости (норма
дисконта)[75].
Напомним, что мы пока не учитываем влияние инфляции на
стоимость денег. Изменение их временнóй стоимости обусловлено лишь
способностью денег оборачиваться и приносить доход.
Рассмотрим для начала простой пример (рис. 5.4)[76]:
Инвестиционным проектом предусматривается
осуществление строительства крупного объекта стоимостью 100 млн. руб. в
течение трех лет. Рассматривается два варианта выполнения работ,
предусматривающих разную схему финансирования проекта по годам:
1 вариант: 1 год –15 млн. руб.;
2 год –25
млн. руб.; 3 год – 60 млн. руб.
2 вариант: 1 год – 20 млн. руб.;
2 год – 40
млн. руб.; 3 год – 40 млн. руб.
Какой вариант финансирования проекта предпочтительнее
для инвестора при прочих равных условиях?
Очевидно, что смысл нашей задачи заключается в том,
что при одинаковой стоимости строительства объекта реальная сумма инвестиций с
учетом временнóй стоимости денег будет разная. Давайте в этом убедимся,
приведя все инвестиции к одной временнóй размерности, т.е. к одному
моменту времени – начальному, то есть началу первого года. Для этого примем
норму дисконта Е=0,1 и определим суммарную приведенную
(дисконтированную) стоимость инвестиций по каждому варианту.

Рис. 5.4.
Распределение инвестиций по вариантам строительства объекта (иллюстрация к
рассматриваемому примеру)

Мы видим, что дисконтированная стоимость инвестиций по
первому варианту меньше на 2,667 млн. руб., чем дисконтированная стоимость
инвестиций по второму варианту. То есть, при одинаковых по обоим вариантам номинальных
затратах инвестора – 100 млн. руб. – с учетом временной стоимости денег реальные
затраты в первом случае будут меньше. Попробуем объяснить это. Мы знаем, что,
инвестируя капитал, инвестор изымает его из текущего оборота, где этот капитал
может приносить доход. А капитал, вложенный в строительство, как бы
«замораживается» – отдача от него начнет поступать только после окончания
строительства и ввода объекта в эксплуатацию. В нашем примере на первом году
строительства объекта в первом варианте было «заморожено» меньше средств, чем
во втором варианте, на 5 млн. руб., следовательно, они продолжали «работать» и
приносить инвестору доход (например, 10 % в год). Аналогично на втором году
строительства – по первому варианту было отвлечено из текущего оборота меньше,
чем по второму варианту на 25 млн. руб. и т.д.
В общем случае при одинаковой сумме инвестиций (в
нашем примере 100 млн. руб.) первый вариант финансирования проекта будет
предпочтительнее второго варианта финансирования проекта (рис. 5.5).
Таким образом, учет временнóй стоимости денег
позволяет сопоставлять разновременные затраты, выбирать варианты инвестирования
с наиболее эффективной схемой финансирования и меньшими приведенными
инвестициями.

Рис. 5.5. Сравнение
вариантов финансирования проекта
[72]
От англ. compound – составной, сложный.
[73]
От англ. discount – учетный процент,
скидка.
[74]
Вам еще не раз придется встретиться с этими коэффициентами, поскольку они имеют
широкое применение не только в инвестиционном анализе, но и в банковских
расчетах, финансовом анализе, в оценке недвижимости и т.д. В разных
литературных источниках норма доходности (дисконта) обозначается разными
символами – R,
r (rate -ставка),
I , i (interest – интерес, процент). Здесь и далее мы будем
использовать обозначения, принятые в «Методических рекомендациях по оценке
эффективности инвестиционных проектов».
[75]
Не случайно в англоязычной литературе норма дисконта (доходности) обозначается
словом rate, которое в переводе на русский язык
имеет два значения: 1) норма, ставка; 2) темп, скорость – см. Мюллер В.К.
Англо-русский словарь: 53 000 слов. – 18-е изд., стереотип. – М.: Рус.
язык., 1981. – 888 с.
[76]
Здесь и далее затраты, в том числе инвестиционные, будем показывать на графиках
как отрицательные величины – ниже оси абсцисс, а доходы как положительные
величины – выше оси абсцисс.
|

